Generalmente los límites pueden hallarse fácilmente, pero pueden aparecer indeterminaciones, o sea, cuantas que matemáticamente no tienen solución. Las más comunes son 0/0 (cero sobre cero) e ∞/∞ (infinito sobre infinito) pero puede hallarse el 0 . ∞ (cero por infinito) ∞ ─ ∞ (infinito menos infinito) 1∞ (Uno elevado a la infinito, que aunque parezca difícil creerlo, no es uno). Para "salvar" estas indeterminaciones y hallar el verdadero valor que se halla escondido dentro de la operación del límite, necesitamos operar matemáticamente, aplicando diversos métodos, desde polinomios hasta logaritmos, inclusive aplicando derivadas (que posiblemente aún no hayas visto). Veremos un ejemplo básico de cada uno de los casos que se te puedan presentar y trataré de explicarlo lo más claro posible... pero como siempre, luego necesitas practicar para poder "dominar" este tema.
Límite tipo 0/0
Empecemos por un limite de polinomios. Para poder resolver y "salvar" la indeterminación lo que necesitas es factorizar el polinomio (tanto el numerador como el denominador) para poder simplificar el binomio que hace cero tanto el numerador (arriba) como el denominador (abajo)
Pasemos al ejercicio.
Ahora debemos ver que el limite sea una indeterminación.
Reemplazamos cada x por el valor al que tiende, 1, y hacemos las cuentas para asegurarnos que tanto el numerador como el denominador nos den cero.
Este procedimiento te evitará trabajar de más (que es lo que todo estudiante desea evitar... )
Ahora procedamos a factorizar ambos polinomios para posteriormente simplificar el binomio que nos hace cero arriba y abajo. Ojo hasta que no simplifiques ambos seguirán dando como resultado cero, por lo que es indispensable "simplificar" para resolver el ejercicio.
Ahora sólo tenemos que reemplazar x por el valor al que tiende y hallar el verdadero valor del límite.
Fíjense que cada vez que reemplazamos x por su valor, no escribimos lim, ya que sólo se escribe cuando está x.
Ahora le toca el turno a las raíces.
Lo primero es ver si hay indeterminación. Reemplacemos cada una de las x por 2 y hacemos las cuentas.
Verifiquemos la indeterminación
La propia x es, en este caso, la causante de la indeterminación, así que podemos factorizarla para poder simplificarla posteriormente.
Ahora procedamos a factorizar ambos polinomios para posteriormente simplificar el binomio que nos hace cero arriba y abajo. Ojo hasta que no simplifiques ambos seguirán dando como resultado cero, por lo que es indispensable "simplificar" para resolver el ejercicio.
Ahora sólo tenemos que reemplazar x por el valor al que tiende y hallar el verdadero valor del límite.
Fíjense que cada vez que reemplazamos x por su valor, no escribimos lim, ya que sólo se escribe cuando está x.
Ahora le toca el turno a las raíces.
Lo primero es ver si hay indeterminación. Reemplacemos cada una de las x por 2 y hacemos las cuentas.
Un vez que hemos comprobado que hay
indeterminación, para salvarla, necesitamos operar
matemáticamente.
El procedimiento es bastante sencillo.
Primeramente podemos
factorizar el binomio del denominador (abajo).
3x – 6 = 3 (x – 2) Siempre nos conviene factorizar, cuando
podemos, ya que nos permitirá simplificar más tarde.
Como hay una raíz, necesitamos
racionalizar, para ello multiplicamos el numerador (arriba) y el denominador
(abajo) por la misma expresión. (Hay que recordar que mientras se mantenga la
igualdad en matemática se puede hacer lo que uno quiere, como es una
multiplicación el uno no altera el resultado, bien, la fracción con el numerador
y el denominador iguales nos dará 1, así que podemos hacer "desaparecer" la raíz
sin que se altere el resultado)
En el numerador (arriba) hacemos distributiva lo que
posteriormente nos permitirá factorizar y hallar el binomio que está anulando
(haciendo cero) la operación. Es el (x – 2) que aparece arriba y abajo
una vez factorizado.
Ojo, siempre necesitamos
simplificarlos para que la indeterminación se vaya.
Después volvemos a reemplazar x
por 2 y, haciendo la cuenta, obtenemos el verdadero valor al que tiende el
límite.
Ahora veamos que sucede cuando x tiende a cero.
Veamos un ejercicio fácil, el procedimiento es el mismo para cualquiera de estos tipos de ejercicios.
Verifiquemos la indeterminación
La propia x es, en este caso, la causante de la indeterminación, así que podemos factorizarla para poder simplificarla posteriormente.
Límite tipo ∞/∞
Para poder resolver este tipo de límites debemos recordar que:
Para resolver este tipo de límites podemos factorizar, pero en este caso (para
que se entienda el por qué) iremos por el camino difícil.
Primeramente
recordemos que en matemática, mientras mantengamos la igualdad, podemos
hacer lo que queramos. En la multiplicación el 1
es el elemento neutro, o sea que multiplicar por uno no modifica nuestro
resultado. El dividir entre sí a 1/x nos da 1, así que podemos
multiplicar por el cociente (división) de 1/x (en el cuadrado
amarillo del ejercicio) lo que nos permitirá (distribuyendo y
simplificando) obtener una operación equivalente que nos permitirá
salvar la indeterminación.
Compliquemos un poco más las cosas.
Muy bien.... ¿Y ahora como procedemos? Cuando nos encontramos frente a
un ejercicio que no hicimos antes buscamos uno parecido que hallamos
resuelto y nos fijamos que hicimos. En el ejercicio anterior dividimos
todo por x, así que volvamos a hacerlo.
O sea que dividir por x no basta ya que el grado del polinomio en
dos, y nos sigue quedando una indeterminación. Así que intentémoslo
nuevamente pero esta vez con x2.
Así que, sencillamente, necesitamos utilizar el grado mayor de cada uno
de los polinomios para salvar la indeterminación. Probemos nuestra
"teoría" con otro ejercicio. (Ojo, para mantener la igualdad debemos
utilizar el mismo grado)
Procedemos, entonces a salvar la indeterminación dividiendo (arriba y
abajo) por una x con el grado máximo del polinomio (x5
en este caso)
Creo que habrán notado que hasta ahora sólo hemos utilizado polinomios
de igual grado en nuestra cuentas, es tiempo de dar otro paso adelante y
ver que sucede cuando los polinomios son de distintos grados. Tenemos
dos opciones, que el de mayor grado esté en el numerador ó que esté en
el denominador.
Veamos la primera opción: mayor grado esté en el numerador.
Ahora veamos que sucede cuando el mayor grado está en el denominador
Así que tenemos tres posibilidades cuando resolvemos limites que tienden
a infinito:
a) Si los polinomios son de igual grado, el límite será finito, (o sea
nos dará un número)
b) Si los polinomios no son de igual grado, y el numerador (arriba) es
el de mayor grado, tendremos como límite a infinito.
c) Si los polinomios no son de igual grado, y el denominador (abajo) es
el de mayor grado, tendremos como límite a cero.


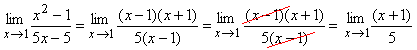


















No hay comentarios.:
Publicar un comentario