Comencemos con un video que explica que la proporción directa tiene una gráfica lineal y se puede expresar como función.
Además se diferencia el gráfico de la función lineal según el conjunto de partida y llegada de la función mostrando como difiere la gráfica en cada caso.
veamos un pequeñisimo video donde se muestran las tres expresiones de la recta lineal:
Ahora analicemos la expresión implícita cuya ecuación es: f(x) = m x + b, donde "b" es un número real al que se lo llama ordenada al origen y "m" (que ya lo conocemos) se denomina pendiente.
Grafiquemos en un par de ejes cartesianos una función lineal
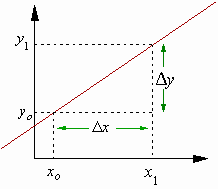
Elegimos dos puntos cualquiera, en este caso (1, 4) y (7, 6). Marcándolos en el gráfico, trazamos una línea punteada desde cada punto hasta sus coordenadas x e y. Así quedará determinado un triángulo rectángulo. Al punto más alejado del centro lo llamaremos (x1; y1); al otro lo llamaremos (xo; yo). Completemos según las coordenadas que elegidas:
xo = 1, yo = 4, x1 = 7, y1 = 6
Marquemos el ángulo que forma la recta con el eje x.
Tomando al ángulo de guía (α) sobre la gráfica velos que el cateto adyacente mide 6 y que es el opuesto mide 2.
¿Qué operación matemática realizamos para calcularlos?
Hemos restado.
La resta (diferencia) se representa por el símbolo D; de allí que al restar x obtuvimos
Δx (se lee diferencial x). Al restar Y obtendremos
Δy ( diferencial y ). De esta manera, el cateto adyacente y el cateto opuesto están representados por
Δx y por Δy respectivamente.
¿Qué función trigonométrica relaciona
Δx y Δy con el ángulo del triángulo?
La tangente.
En este caso ¿Qué valor tiene ?
Es importante notar que entre dos puntos cuales quiera que pertenezcan a la recta, puede trazarse un triángulo rectángulo, de manera que, la razón de sus catetos sea 1/3, el valor de la pendiente.
Para poder calcular la ecuación de esta recta sólo nos falta saber el valor de la ordenada al origen "b" .
La ecuación de la recta es: y = m x + b
Elijamos uno de los puntos de la recta, (1, 4) y suplantemos " x e y " con ellos en la ecuación: 4 = m. 1 + b
Hagamos lo mismo con el valor de "m" (la pendiente):
Despejemos b para hallar su valor:
De esa manera la ecuación de la recta que pasa por (1, 4) y (7, 6) es:
Volviendo al triángulo que quedó formado en el gráfico:
Aún queda, sin saber su medida, la hipotenusa del triángulo; ese lado coincide con la distancia entre los dos puntos marcados. El teorema de Pitágoras nos permite conocer esa medida.
Distancia entre dos puntos: D2 =
Δx2 + Δy2
Graficar una recta (sin tabla)
Para graficar una recta se deben tener en cuenta la pendiente de la misma y la ordenada al origen.
Grafiquemos la recta: y = 3 x + 1
La ordenada al origen es (0, 1), el o primero que ubicamos en el gráfico. A partir de ese punto aplicamos el concepto de pendiente, subimos tres (por que el valor es positivo, sentido positivo del eje y; de ser negativo bajaríamos) y corremos uno hacia la derecha (sentido positivo del eje de las x). Por esos dos puntos trazamos la recta.
Ejercitación
1) Determinar la ecuación de la recta que posee pendiente m = 2 y pasa
por el punto (5; –1)
Rta.: y = 2x – 11
2) Escribir las ecuaciones de las rectas determinadas por cada uno de los
siguientes pares de puntos (0 ; 7) y (– 2 ; 1)
Rta.: y = 3x + 7
3) Escribir las ecuaciones de las rectas que contienen a cada uno de los
lados del triángulo cuyos vértices son: ( 2 ; 1); (0 ; 2) y (– 3 ; – 4)
Rta.: y = – 2x + 2; y = – x + 2; y
= x – 1
4) Escribir la ecuación de la recta paralela y perpendicular a y
= – ½ x + 1 que pase por el punto P = ( 4 ; 0)
Rta.: y = – ½ x + 2; y = 2x
– 8
5) Determinar la distancia entre los puntos (1;2) y (4;6)
Rta.: 5
6) Calcular el perímetro de las siguientes figuras.
Rta.: 62,44 ; 49,88.

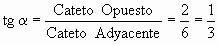






No hay comentarios.:
Publicar un comentario