Imagínate que sufres una pesadilla (por tanto estudiar matemática) en la que te encuentras durmiendo en tu habitación y tu cama se halla cerca de una puerta. Ante la urgencia de ir al baño, te levantas y te acercas a la puerta para abrirla. Caminas hacia ella y estiras el brazo para agarrar el picaporte. A medida que caminas te percatas que estas cada vez más cerca, pero no alcanzas a tocar el picaporte. Comienzas a desesperarte y empiezas a correr tratando de agarrarlo, pero, no puedes. No importa cuanto lo intentes siempre hay un espacio entre tu mano y el picaporte, aunque ese espacio se reduce y se hace más pequeño a medida que avanzas, te das cuenta que jamás tocarás el picaporte.
Esa "pesadilla" tiene nombre matemático "límite".
Esa "pesadilla" tiene nombre matemático "límite".
Desde el punto de vista del conjunto de los números reales, que es denso (infinito e infinitésimo), podemos encontrar entre dos números consecutivos infinitos números: tomemos dos números, por ejemplo, 4 y 5, busquemos un número real entre ellos, podemos tomar 4,5 que está entre 4 y 5
4 .... 4,5 ..... 5
Ahora busquemos un número entre 4 y 4,5
(podemos tomar 4,3 que está entre 4 y 4,5)
4 ...... 4,3 ..... 4,5
Ahora busquemos un número entre 4 y 4,3
(podemos tomar 4,1 que está entre 4 y 4,3)
4 ....... 4,1 ...... 4,3
Ahora busquemos un número entre 4 y 4,1
(podemos tomar 4,08 que está entre 4 y 4,1)
4 ...... 4,08 .... 4,1
Ahora busquemos un número entre 4 y 4,08
(podemos tomar 4,001 que está entre 4 y 4,08)
4 ..... 4,001 .... 4,08
Podemos seguir así eternamente. Siempre nos podremos acercar al número "4" todo
lo que queramos sin llegar a él. Justamente "4" es el límite que no podemos
tocar. Como nos acercamos desde valores mayores a 4, se dice que nos "acercamos
por la derecha".
Si nos acercáramos con valores más pequeños, nos "acercaríamos por la izquierda".
El concepto de límite está íntimamente
ligado al concepto de
función. Cada uno de los
números que se acerca a 4 pueden obtenerse de una ecuación (lineal por ejemplo)
como y = 4 + x. Donde al darle
valores a x obtenemos "esos" números que se acercan a 4 por derecha e
izquierda. Evidentemente, de acuerdo al tipo de ecuación que tengamos, serán los
valores de x a tomar en cuenta.
En este caso no nos interesa cuando
x = 0, ya que no queremos que "la cuenta" de 4 (que es nuestro límite).
|
← Por
izquierda
Por derecha →
|
|
El valor de x se acerca a
"cero" y el valor de "y" (la imagen de la función) se acerca a 4. Para
hablar con propiedad, en matemática no se dice "se acerca a" sino "tiende a";
x tiende a cero cuando
y tiende a cuatro. Es real, a los que hacemos matemática no nos
gusta escribir mucho. Se reemplaza las palabras con símbolos para ahorrar tiempo
(el esfuerzo mental se reserva para el problema matemático). Así que en vez de
escribir "tiende a" se pone una flecha. De manera que "x
tiende a cero" se indica "x ® 0" e "y
tiende a cuatro" se escribe como "y →
4".
Ya estamos un poco más cerca de poder
leer "matemáticamente". El límite (lím) suele escribirse indicando debajo de él
el valor a que tiende x, seguido de la ecuación que se analiza y (después
del igual) se indica el valor del límite.
No siempre los límites laterales (izquierda y derecha) son iguales. Analicemos
la siguiente función.
Para hallar el límite de esta función
(paramétrica) debemos separar la parte de la ecuación que se utiliza para
valores menores o iguales que "1", (x + 3), de la parte que se utiliza
con los valores mayores a "1", o sea, (x – 1).
Nuevamente (para escribir menos)
indicamos con el signo "+" (colocado como superíndice en el lado derecho del
número a que tiende x) cuando analizamos una función desde la derecha.
Para Calcular el límite, sencillamente reemplazamos "x" por el número a
que tiende:
Indicamos con el signo"–" (colocado
como superíndice en el lado derecho del número a que tiende x) cuando
analizamos una función desde la izquierda. Para Calcular el límite,
sencillamente reemplazamos "x" por el número a que tiende:
Los límites laterales (izquierda y derecha) no son iguales, entonces, la función
no tiene límite en x = 1.
Probemos con otra función y analicemos
los límites laterales; si ellos dan lo mismo, el límite de la función es ese
valor.
Presupongo
que para la mayoría que esté leyendo este artículo, leer esta definición
se asemeja mucho a tratar de descifrar un texto en sánscrito, por lo que
traduciré lo que significa.
La definición nos habla de un
intervalo (a, b) dentro del cual hallamos el valor de
xo que buscamos. No nos sirve que esté fuera ya que
queremos indicar claramente donde podemos encontrarlo. Si decimos que
xo pertenece al intervalo (1, 2) ella
tiene muchos valores
posibles pero siempre será mayor que 1 y menor que 2. Así que cuanto más
pequeño sea el intervalo, mejor "definido" estará el valor de xo.
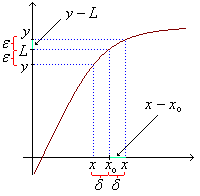
Justamente la distancia entre a y xo se denomina
δ. Como a y b son valores de x esa distancia (que
la calculamos como una resta) se escribe x – xo.
Lo mismo sucede en la imagen, pero en este caso el radio del entorno reducido se denomina ε. Así que ∀ε > 0, se traduce como: para todo épsilon que es mayor que cero. Nuevamente tenemos una distancia pequeña y positiva que corresponde a las imágenes. Donde antes teníamos a x ahora encontramos a f(x), donde estaba xo ahora nos encontramos con su imagen L, así tenemos que
Entonces ahora traduzcamos la definición de límites:
Definición matemática de límite
Hemos visto
que el proceso de límite es un "acercamiento perpetuo" a un valor
determinado de x (al que llamaremos xo) en una
función, sin importarnos cual sea la imagen de x.
Para poder
entender el proceso de límite necesitamos utilizar nuestra imaginación,
buscando una metáfora del proceso de límite, podríamos compararlo con la
llegada de un tren a la estación. No nos importa que estación sea ni
cómo se llame, ni siquiera como es la estación. Lo único que nos
interesa cómo se acerca el tren (de cualquiera de los dos lados).
Si bien la
definición de límite puede variar mínimamente de un libro a otro, vamos
a encontrar la misma estructura en cada uno de ellos y (generalmente) se
utilizan las mismas letras para no crear confusión. En este caso
utilizaré la definición que se encuentra en el libro de análisis
matemático I de la cátedra Thomson de ciencias económicas de la
Universidad de Buenos Aires (UBA) (2008)
Sea f una función
definida en todos los puntos del intervalo (a, b), salvo
quizás en xo perteneciente a (a, b).
Decimos que f(x) tiene límite L cuando
x se acerca a xo notándolo (escribiéndolo como) :
La definición nos habla de un
intervalo (a, b) dentro del cual hallamos el valor de
xo que buscamos. No nos sirve que esté fuera ya que
queremos indicar claramente donde podemos encontrarlo. Si decimos que
xo pertenece al intervalo (1, 2) ella
tiene muchos valores
posibles pero siempre será mayor que 1 y menor que 2. Así que cuanto más
pequeño sea el intervalo, mejor "definido" estará el valor de xo.
Justamente la distancia entre a y xo se denomina
δ. Como a y b son valores de x esa distancia (que
la calculamos como una resta) se escribe x – xo.
Nos interesa el valor de la distancia por lo que la operación se
encierra en un módulo (valor absoluto).
Así δ es la distancia entre xo y cualquiera de los
extremos del intervalo que lo contiene. Cuando se escribe ∃δ > 0, se
quiere decir que existe una δ cuyo valor es positivo (mayor que cero)
ya que representa una distancia.
Cuando se escribe: 0 < | x – xo.| < δ, se está diciendo que ese valor lo calculamos restando los extremos del
intervalo con el valor medio que representa xo.
Determinando un entorno reducido cuyo radio es δ.
Lo mismo sucede en la imagen, pero en este caso el radio del entorno reducido se denomina ε. Así que ∀ε > 0, se traduce como: para todo épsilon que es mayor que cero. Nuevamente tenemos una distancia pequeña y positiva que corresponde a las imágenes. Donde antes teníamos a x ahora encontramos a f(x), donde estaba xo ahora nos encontramos con su imagen L, así tenemos que
|f(x) – L| < ε
Entonces ahora traduzcamos la definición de límites:
Tenemos un
límite de x tendiendo a xo cuyo límite es L,
si y sólo si, para todo valor de épsilon mayor que cero, existe un valor
delta, también mayor a cero, de manera que la diferencia (recta) entre
x y xo sea positiva y menor a delta, entonces,
hallaremos una diferencia entre f(x) y L
de manera que sea menor a épsilon.
Esta
definición relaciona los radios de los entornos reducidos entre sí y nos
permite "elegir" cuan pequeños queremos que sea ese intervalo. δ se
halla sobre el eje x, mientras que ε se halla sobre el eje
y.
Otra
pregunta frecuente es ¿para que nos sirve todo esto?....
Para
contestar esta pregunta, nuevamente, necesitas imaginación, ya que δ, ε,
x, f(x) carecen de significado, y pueden
representar muchas cosas.
Imaginemos
que estamos investigando la acción de una droga en pacientes oncológicos
(que padecen cáncer).x puede representar la cantidad administrada
de un medicamento, mientras que y (f(x))
representa la presión sanguínea generada por el medicamento. Así pues,
xo es la dosis que produce una presión L que puede
producir un derrame cerebral en el paciente, pero que elimina
eficazmente las células cancerígenas. Aquí adquiere gran importancia δ y
ε, queremos acercarnos pero no llegar. Para eso sirve el
proceso de límite (en este caso un límite desde la izquierda que tiende
a valores menores de xo)
Aplicaciones de límites en diversas funciones matemáticas
Los límites tienen muchas aplicaciones, una de ellas se ejemplifica en las funciones Homográficas cuya ecuación canónica puede escribirse como:
De las que tenemos que tenemos la definición de asíntotas (horizontal, vertical y
oblicua) cuya explicación se encuentra en dichas
funciones.
Cuando el límite (de x tendiendo a un valor que depende de la función, por eso la llamamos "a")
por izquierda y por derecha tiende a infinito; característica que define a la
asíntota vertical.
Cuando el límite (de x
tendiendo a infinito por izquierda "– ¥" y por
derecha "+ ¥") tiende a un valor que depende de la
función, por eso la llamamos "b"; característica que define a la asíntota
horizontal.
Si a = 0 y b = 0,
podemos reducir a los conocidos
(ver desarrollo en
función homográfica)
Limites de funciones exponenciales
Ver funciones exponenciales y logarítmicas primero.
Otra aplicación de límites podemos hallarlas en las ecuaciones exponenciales de tipo
Limites de funciones exponenciales
Ver funciones exponenciales y logarítmicas primero.
Otra aplicación de límites podemos hallarlas en las ecuaciones exponenciales de tipo
que nos permitirá hallar el valor de e, la base de
los logaritmos neperianos o naturales.
Es de destacar que el intervalo [–1,
0] no pertenece al
dominio de la función (queda
en ustedes averiguar por qué).
A medida que x se hace más
grande, tiende a infinito positivo (x ® +¥)
la imagen "se acerca a un valor" 2,718281828 ... (número irracional) que se lo
denomina e. De igual manera, si tomamos
valores de x cada vez más chiquitos, tiende a infinito negativo (x
® - ¥) la imagen también "se acerca al mismo valor"
e.
Otra aplicación similar podemos
hallarla en las funciones cuya ecuación exponencial es del tipo f
(x) = (1 + x)1/x.
Nuevamente
el dominio está restringido, en este caso, a valores mayores a – 1. Si hacemos
que x tienda a cero, por izquierda y por derecha, el valor del límite
(las imágenes que obtenemos al resolver la ecuación con cada valor de x
elegido) también dará como resultado e.
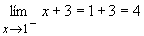
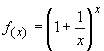
No hay comentarios.:
Publicar un comentario